- name : detic
- category : misc
Objective
The goal of this challenge is to find a point on Earth that is equidistant from three given locations on earth.
When we connect to the instance, we get the following message:
| Hi, as a `ASIS` driver, you should be in a position where you are |
| exactly the same distance from three passengers in Iran. We will |
| calculate this distance with an accuracy of ten meters. For this, |
| assume that the earth is completely spherical and its radius is |
| exactly 6371 km. Hence, in each step you should find the precise |
| langitude and altitue and send to server separeted with comma. |
| Are you ready? please send [Y]es or [N]o. |
By answering Y, we are given 3 coordinates as longitude and latitude:
| Consider the following three locations in Iran:
| P1 = ('OWLTAN_CASTLE', (39.60960517227403, 47.75964978116872))
| P2 = ('MOZDORAN_CAVE', (36.15158614723986, 60.54987387810325))
| P3 = ('KUHE_SIAHAN', (27.22154699581871, 62.88183831028374))
| Please send a point with same distance to the above points like x, y:
After having the desired arguments, we need to think about how to calculate the center of these 3 coordinates.
The main difficulty of this challenge is the fact that we are dealing with coordinates in degrees (latitude, longitude) on a sphere.
While it is easy to find the middle of a triangle in a two dimmensional plane, the calculation reveals itself to be more complex when dealing with a sherical surface.
‘Naive’ method
First of all, we will need to convert our coordinates to carthesian coordinates. To do this, we create the following functions:
def lat_lon_to_cartesian(lat, lon):
lat = numpy.radians(lat)
lon = numpy.radians(lon)
x = EARTH_RADIUS * numpy.cos(lat) * numpy.cos(lon)
y = EARTH_RADIUS * numpy.cos(lat) * numpy.sin(lon)
z = EARTH_RADIUS * numpy.sin(lat)
return (x, y, z)
def cartesian_to_lat_lon(x, y, z):
r = numpy.sqrt(x*x+y*y+z*z)
# print(f"known radius :{EARTH_RADIUS}\nrecalculated radius:{r}")
lon = numpy.arctan2(y, x)
lat = numpy.arcsin(z / r)
return (numpy.degrees(lat), numpy.degrees(lon))
Our initial attempt is to get the middle coordinates of these three points, then normalize it and then multiply it by the radius of the earth.
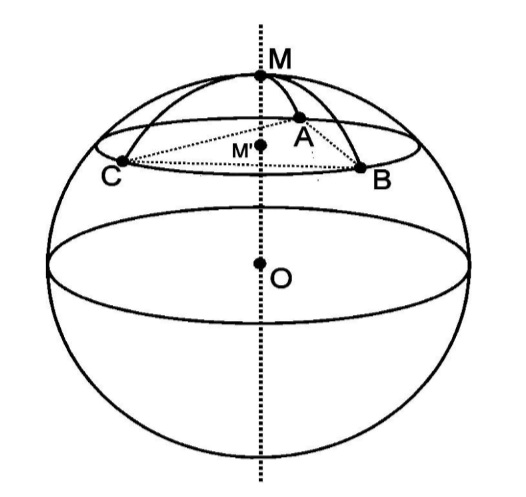
def normalize(x,y,z):
lenght = numpy.sqrt(x**2+y**2+z**2)
return (x / lenght, y / lenght, z / lenght)
def solve(P1,P2,P3):
A = lat_lon_to_cartesian(*P1)
B = lat_lon_to_cartesian(*P2)
C = lat_lon_to_cartesian(*P3)
M = ((A[0]+B[0]+C[0])/3,(A[1]+B[1]+C[1])/3,(A[2]+B[2]+C[2])/3)
M = normalize(*M)
# print(f"coordinates:{M[0]}:{M[1]}:{M[2]}")
return cartesian_to_lat_lon(M[0]*EARTH_RADIUS,M[1]*EARTH_RADIUS,M[2]*EARTH_RADIUS)
While the given result is coherent, it is not what is expected by the instance, and so the search continues.
The right method
We then find this article, that explains how to compute a geographic midpoint with a given number of coordinates, but not a geometrical midpoint, which is instead what we’re looking for.
After further research, we found this paper on spherical geometry, which provides the formula we were looking for.
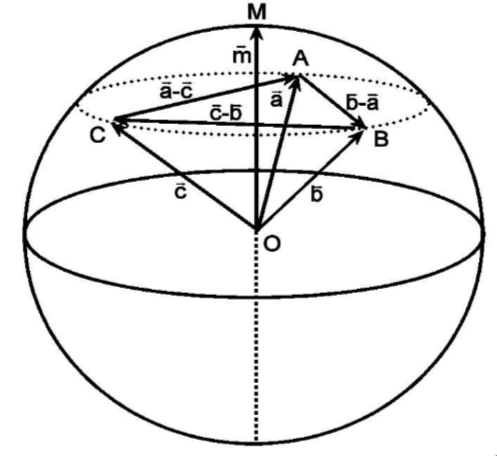
By applying the described calculations, we get the following code:
def appendix(P1,P2,P3):
(xa,ya,za) = lat_lon_to_cartesian(*P1)
(xb,yb,zb) = lat_lon_to_cartesian(*P2)
(xc,yc,zc) = lat_lon_to_cartesian(*P3)
print(f"coordinates:\nx{xa}:{ya}:{za}\ny:{xb}:{yb}:{zb}\nc:{xc}:{yc}:{zc}")
axb = (ya*zb - za*yb,za*xb - xa*zb, xa*yb - ya*xb)
bxc = (yb*zc - zb*yc,zb*xc - xb*zc, xb*yc - yb*xc)
cxa = (yc*za - zc*ya,zc*xa - xc*za, xc*ya - yc*xa)
m = (axb[0]+bxc[0]+cxa[0],axb[1]+bxc[1]+cxa[1],axb[2]+bxc[2]+cxa[2])
return cartesian_to_lat_lon(*m)
The first calculation is now done, and validated by the instance ! By repeating these steps, the flag is obtained.
Solver script
from pwn import remote
import numpy, re
EARTH_RADIUS = 6371
def lat_lon_to_cartesian(lat, lon):
lat = numpy.radians(lat)
lon = numpy.radians(lon)
x = EARTH_RADIUS * numpy.cos(lat) * numpy.cos(lon)
y = EARTH_RADIUS * numpy.cos(lat) * numpy.sin(lon)
z = EARTH_RADIUS * numpy.sin(lat)
return (x, y, z)
def cartesian_to_lat_lon(x, y, z):
r = numpy.sqrt(x*x+y*y+z*z)
lon = numpy.arctan2(y, x)
lat = numpy.arcsin(z / r)
return (numpy.degrees(lat), numpy.degrees(lon))
def appendix(P1,P2,P3):
(xa,ya,za) = lat_lon_to_cartesian(*P1)
(xb,yb,zb) = lat_lon_to_cartesian(*P2)
(xc,yc,zc) = lat_lon_to_cartesian(*P3)
axb = (ya*zb - za*yb,za*xb - xa*zb, xa*yb - ya*xb)
bxc = (yb*zc - zb*yc,zb*xc - xb*zc, xb*yc - yb*xc)
cxa = (yc*za - zc*ya,zc*xa - xc*za, xc*ya - yc*xa)
m = (axb[0]+bxc[0]+cxa[0],axb[1]+bxc[1]+cxa[1],axb[2]+bxc[2]+cxa[2])
return cartesian_to_lat_lon(*m)
# initiating the remote instance
r = remote("65.109.192.143", 13770)
r.settimeout(5)
r.sendline(b"Y")
while True:
try:
res = r.recvuntil(b"Please send a point with same distance to the above points like x, y:").decode()
# print(res)
pattern = re.compile(r"\(([\d\.\-]+), ([\d\.\-]+)\)")
matches = pattern.findall(res)
P1_lat, P1_lon = matches[0]
P2_lat, P2_lon = matches[1]
P3_lat, P3_lon = matches[2]
P1 = (float(P1_lat), float(P1_lon))
P2 = (float(P2_lat), float(P2_lon))
P3 = (float(P3_lat), float(P3_lon))
centroid_lat, centroid_lon = appendix(P1,P2,P3)
rounded_answer = f"{round(centroid_lat, 14)},{round(centroid_lon, 14)}"
# print("Answer:", rounded_answer)
r.sendline(rounded_answer.encode())
except:
while True:
try:
print(r.recv().decode())
except:
exit()
Acknowledgements
Thanks to nekro for setting up the script and giving some hints, check out his writeup